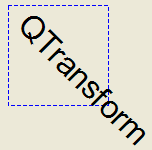
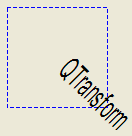
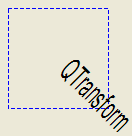
QTransform¶

PyQt5.QtGui.QTransform

Description¶

The QTransform class specifies 2D transformations of a coordinate system.

A transformation specifies how to translate, scale, shear, rotate or project the coordinate system, and is typically used when rendering graphics.

QTransform differs from QMatrix in that it is a true 3x3 matrix, allowing perspective transformations. QTransform’s toAffine() method allows casting QTransform to QMatrix. If a perspective transformation has been specified on the matrix, then the conversion will cause loss of data.

QTransform is the recommended transformation class in Qt.

A QTransform object can be built using the setMatrix(), scale(), rotate(), translate() and shear() functions. Alternatively, it can be built by applying basic matrix operations. The matrix can also be defined when constructed, and it can be reset to the identity matrix (the default) using the reset() function.

The QTransform class supports mapping of graphic primitives: A given point, line, polygon, region, or painter path can be mapped to the coordinate system defined by this matrix using the map() function. In case of a rectangle, its coordinates can be transformed using the mapRect() function. A rectangle can also be transformed into a polygon (mapped to the coordinate system defined by this matrix), using the mapToPolygon() function.

QTransform provides the isIdentity() function which returns true if the matrix is the identity matrix, and the isInvertible() function which returns true if the matrix is non-singular (i.e. AB = BA = I). The inverted() function returns an inverted copy of this matrix if it is invertible (otherwise it returns the identity matrix), and adjoint() returns the matrix’s classical adjoint. In addition, QTransform provides the determinant() function which returns the matrix’s determinant.

Finally, the QTransform class supports matrix multiplication, addition and subtraction, and objects of the class can be streamed as well as compared.

Rendering Graphics¶

When rendering graphics, the matrix defines the transformations but the actual transformation is performed by the drawing routines in QPainter.

By default, QPainter operates on the associated device’s own coordinate system. The standard coordinate system of a QPaintDevice has its origin located at the top-left position. The x values increase to the right; y values increase downward. For a complete description, see the coordinate system documentation.

QPainter has functions to translate, scale, shear and rotate the coordinate system without using a QTransform. For example:

image-qtransform-simpletransformation-png

# void SimpleTransformation::paintEvent(QPaintEvent *)
# {
#     QPainter painter(this);
#     painter.setPen(QPen(Qt::blue, 1, Qt::DashLine));
#     painter.drawRect(0, 0, 100, 100);

#     painter.rotate(45);

#     painter.setFont(QFont("Helvetica", 24));
#     painter.setPen(QPen(Qt::black, 1));
#     painter.drawText(20, 10, "QTransform");
# }

Although these functions are very convenient, it can be more efficient to build a QTransform and call setTransform() if you want to perform more than a single transform operation. For example:

image-qtransform-combinedtransformation-png

# void CombinedTransformation::paintEvent(QPaintEvent *)
# {
#     QPainter painter(this);
#     painter.setPen(QPen(Qt::blue, 1, Qt::DashLine));
#     painter.drawRect(0, 0, 100, 100);

#     QTransform transform;
#     transform.translate(50, 50);
#     transform.rotate(45);
#     transform.scale(0.5, 1.0);
#     painter.setTransform(transform);

#     painter.setFont(QFont("Helvetica", 24));
#     painter.setPen(QPen(Qt::black, 1));
#     painter.drawText(20, 10, "QTransform");
# }

Basic Matrix Operations¶

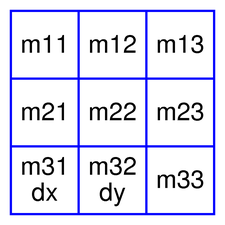
../../_images/qtransform-representation.png

A QTransform object contains a 3 x 3 matrix. The m31 (dx) and m32 (dy) elements specify horizontal and vertical translation. The m11 and m22 elements specify horizontal and vertical scaling. The m21 and m12 elements specify horizontal and vertical shearing. And finally, the m13 and m23 elements specify horizontal and vertical projection, with m33 as an additional projection factor.

QTransform transforms a point in the plane to another point using the following formulas:

# x' = m11*x + m21*y + dx
# y' = m22*y + m12*x + dy
# if (is not affine) {
#     w' = m13*x + m23*y + m33
#     x' /= w'
#     y' /= w'
# }

The point (x, y) is the original point, and (x’, y’) is the transformed point. (x’, y’) can be transformed back to (x, y) by performing the same operation on the inverted() matrix.

The various matrix elements can be set when constructing the matrix, or by using the setMatrix() function later on. They can also be manipulated using the translate(), rotate(), scale() and shear() convenience functions. The currently set values can be retrieved using the m11(), m12(), m13(), m21(), m22(), m23(), m31(), m32(), m33(), dx() and dy() functions.

Translation is the simplest transformation. Setting dx and dy will move the coordinate system dx units along the X axis and dy units along the Y axis. Scaling can be done by setting m11 and m22. For example, setting m11 to 2 and m22 to 1.5 will double the height and increase the width by 50%. The identity matrix has m11, m22, and m33 set to 1 (all others are set to 0) mapping a point to itself. Shearing is controlled by m12 and m21. Setting these elements to values different from zero will twist the coordinate system. Rotation is achieved by setting both the shearing factors and the scaling factors. Perspective transformation is achieved by setting both the projection factors and the scaling factors.

Here’s the combined transformations example using basic matrix operations:

image-qtransform-combinedtransformation2-png

# void BasicOperations::paintEvent(QPaintEvent *)
# {
#     double pi = 3.14;

#     double a    = pi/180 * 45.0;
#     double sina = sin(a);
#     double cosa = cos(a);

#     QTransform translationTransform(1, 0, 0, 1, 50.0, 50.0);
#     QTransform rotationTransform(cosa, sina, -sina, cosa, 0, 0);
#     QTransform scalingTransform(0.5, 0, 0, 1.0, 0, 0);

#     QTransform transform;
#     transform = scalingTransform * rotationTransform * translationTransform;

#     QPainter painter(this);
#     painter.setPen(QPen(Qt::blue, 1, Qt::DashLine));
#     painter.drawRect(0, 0, 100, 100);

#     painter.setTransform(transform);

#     painter.setFont(QFont("Helvetica", 24));
#     painter.setPen(QPen(Qt::black, 1));
#     painter.drawText(20, 10, "QTransform");
# }

Enums¶

TransformationType

Member	Value	Description
TxNone	TODO	TODO
TxProject	TODO	TODO
TxRotate	TODO	TODO
TxScale	TODO	TODO
TxShear	TODO	TODO
TxTranslate	TODO	TODO

Methods¶

__init__()

Constructs an identity matrix.

All elements are set to zero except m11 and m22 (specifying the scale) and m33 which are set to 1.

See also

reset().

__init__(QTransform): TODO

__init__(float, float, float, float, float, float): TODO

__init__(float, float, float, float, float, float, float, float, m33: float = 1): TODO

__add__(float) → QTransform: TODO

adjoint() → QTransform: Returns the adjoint of this matrix.

determinant() → float: TODO

dx() → float: TODO

dy() → float: TODO

__eq__(QTransform) → bool: TODO

@staticmethod fromScale(float, float) → QTransform: Creates a matrix which corresponds to a scaling of sx horizontally and sy vertically. This is the same as QTransform.scale(sx, sy) but slightly faster.

@staticmethod fromTranslate(float, float) → QTransform: Creates a matrix which corresponds to a translation of dx along the x axis and dy along the y axis. This is the same as QTransform.translate(dx, dy) but slightly faster.

__hash__() → int: TODO

__iadd__(float) → QTransform: TODO

__imatmul__(QTransform) → QTransform: TODO

__imul__(QTransform) → QTransform: TODO

__imul__(float) → QTransform: TODO

inverted() → (QTransform, bool)

Returns an inverted copy of this matrix.

If the matrix is singular (not invertible), the returned matrix is the identity matrix. If invertible is valid (i.e. not 0), its value is set to true if the matrix is invertible, otherwise it is set to false.

See also

isInvertible().

isAffine() → bool: TODO

isIdentity() → bool: TODO

isInvertible() → bool: TODO

isRotating() → bool: TODO

isScaling() → bool: TODO

isTranslating() → bool: TODO

__isub__(float) → QTransform: TODO

__itruediv__(float) → QTransform: TODO

m11() → float: TODO

m12() → float: TODO

m13() → float: TODO

m21() → float: TODO

m22() → float: TODO

m23() → float: TODO

m31() → float: TODO

m32() → float: TODO

m33() → float: TODO

map(QPoint) → QPoint: TODO

map(Union[QPointF, QPoint]) → QPointF: TODO

map(QLine) → QLine: TODO

map(QLineF) → QLineF: TODO

map(QPolygonF) → QPolygonF: TODO

map(QPolygon) → QPolygon: TODO

map(QRegion) → QRegion: TODO

map(QPainterPath) → QPainterPath

This is an overloaded function.

Creates and returns a QPainterPath object that is a copy of the given path, mapped into the coordinate system defined by this matrix.

map(int, int) → (int, int)

This is an overloaded function.

Maps the given coordinates x and y into the coordinate system defined by this matrix. The resulting values are put in *tx and *ty, respectively. Note that the transformed coordinates are rounded to the nearest integer.

map(float, float) → (float, float)

Maps the given coordinates x and y into the coordinate system defined by this matrix. The resulting values are put in *tx and *ty, respectively.

The coordinates are transformed using the following formulas:

# x' = m11*x + m21*y + dx
# y' = m22*y + m12*x + dy
# if (is not affine) {
#     w' = m13*x + m23*y + m33
#     x' /= w'
#     y' /= w'
# }

The point (x, y) is the original point, and (x’, y’) is the transformed point.

See also

Basic Matrix Operations.

mapRect(QRect) → QRect: TODO

mapRect(QRectF) → QRectF: TODO

mapToPolygon(QRect) → QPolygon: TODO

__matmul__(QTransform) → QTransform: TODO

__mul__(QTransform) → QTransform: TODO

__mul__(float) → QTransform: TODO

__ne__(QTransform) → bool: TODO

@staticmethod quadToQuad(QPolygonF, QPolygonF, QTransform) → bool

Creates a transformation matrix, trans, that maps a four-sided polygon, one, to another four-sided polygon, two. Returns true if the transformation is possible; otherwise returns false.

This is a convenience method combining quadToSquare() and squareToQuad() methods. It allows the input quad to be transformed into any other quad.

See also

squareToQuad(), quadToSquare().

@staticmethod quadToSquare(QPolygonF, QTransform) → bool: TODO

reset(): TODO

rotate(float, axis: Axis = ZAxis) → QTransform: TODO

rotateRadians(float, axis: Axis = ZAxis) → QTransform: TODO

scale(float, float) → QTransform: Scales the coordinate system by sx horizontally and sy vertically, and returns a reference to the matrix.

See also

setMatrix().

setMatrix(float, float, float, float, float, float, float, float, float): Sets the matrix elements to the specified values, m11, m12, m13 m21, m22, m23 m31, m32 and m33. Note that this function replaces the previous values. QTransform provides the translate(), rotate(), scale() and shear() convenience functions to manipulate the various matrix elements based on the currently defined coordinate system.

See also

QTransform.

shear(float, float) → QTransform: Shears the coordinate system by sh horizontally and sv vertically, and returns a reference to the matrix.

See also

setMatrix().

@staticmethod squareToQuad(QPolygonF, QTransform) → bool: Creates a transformation matrix, trans, that maps a unit square to a four-sided polygon, quad. Returns true if the transformation is constructed or false if such a transformation does not exist.

See also

quadToSquare(), quadToQuad().

__sub__(float) → QTransform: TODO

translate(float, float) → QTransform: Moves the coordinate system dx along the x axis and dy along the y axis, and returns a reference to the matrix.

See also

setMatrix().

transposed() → QTransform: Returns the transpose of this matrix.

__truediv__(float) → QTransform: TODO

type() → TransformationType

Returns the transformation type of this matrix.

The transformation type is the highest enumeration value capturing all of the matrix’s transformations. For example, if the matrix both scales and shears, the type would be TxShear, because TxShear has a higher enumeration value than TxScale.

Knowing the transformation type of a matrix is useful for optimization: you can often handle specific types more optimally than handling the generic case.