QEasingCurve

PyQt5.QtCore.QEasingCurve

Description

The QEasingCurve class provides easing curves for controlling animation.

Easing curves describe a function that controls how the speed of the interpolation between 0 and 1 should be. Easing curves allow transitions from one value to another to appear more natural than a simple constant speed would allow. The QEasingCurve class is usually used in conjunction with the QVariantAnimation and QPropertyAnimation classes but can be used on its own. It is usually used to accelerate the interpolation from zero velocity (ease in) or decelerate to zero velocity (ease out). Ease in and ease out can also be combined in the same easing curve.

To calculate the speed of the interpolation, the easing curve provides the function valueForProgress(), where the progress argument specifies the progress of the interpolation: 0 is the start value of the interpolation, 1 is the end value of the interpolation. The returned value is the effective progress of the interpolation. If the returned value is the same as the input value for all input values the easing curve is a linear curve. This is the default behaviour.

For example,

#     QEasingCurve easing(QEasingCurve::InOutQuad);

#     for (qreal t = 0.0; t < 1.0; t += 0.1)
#         qWarning() << "Effective progress" << t << "is"
#                    << easing.valueForProgress(t);

will print the effective progress of the interpolation between 0 and 1.

When using a QPropertyAnimation, the associated easing curve will be used to control the progress of the interpolation between startValue and endValue:

#     QPropertyAnimation animation;
#     animation.setStartValue(0);
#     animation.setEndValue(1000);
#     animation.setDuration(1000);
#     animation.setEasingCurve(QEasingCurve::InOutQuad);

The ability to set an amplitude, overshoot, or period depends on the QEasingCurve type. Amplitude access is available to curves that behave as springs such as elastic and bounce curves. Changing the amplitude changes the height of the curve. Period access is only available to elastic curves and setting a higher period slows the rate of bounce. Only curves that have “boomerang” behaviors such as the InBack, OutBack, InOutBack, and OutInBack have overshoot settings. These curves will interpolate beyond the end points and return to the end point, acting similar to a boomerang.

The Easing Curves Example contains samples of QEasingCurve types and lets you change the curve settings.

Enums

Type

The type of easing curve.

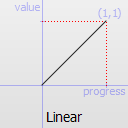
Easing curve for a linear (t) function: velocity is constant.

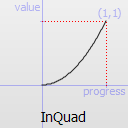
Easing curve for a quadratic (t^2) function: accelerating from zero velocity.

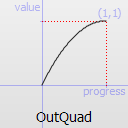
Easing curve for a quadratic (t^2) function: decelerating to zero velocity.

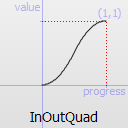
Easing curve for a quadratic (t^2) function: acceleration until halfway, then deceleration.

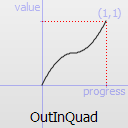
Easing curve for a quadratic (t^2) function: deceleration until halfway, then acceleration.

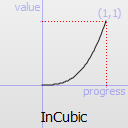
Easing curve for a cubic (t^3) function: accelerating from zero velocity.

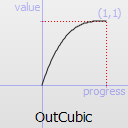
Easing curve for a cubic (t^3) function: decelerating to zero velocity.

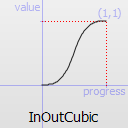
Easing curve for a cubic (t^3) function: acceleration until halfway, then deceleration.

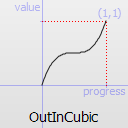
Easing curve for a cubic (t^3) function: deceleration until halfway, then acceleration.

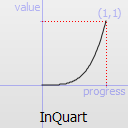
Easing curve for a quartic (t^4) function: accelerating from zero velocity.

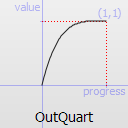
Easing curve for a quartic (t^4) function: decelerating to zero velocity.

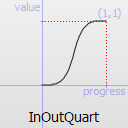
Easing curve for a quartic (t^4) function: acceleration until halfway, then deceleration.

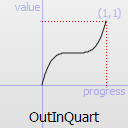
Easing curve for a quartic (t^4) function: deceleration until halfway, then acceleration.

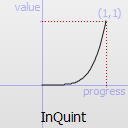
Easing curve for a quintic (t^5) easing in: accelerating from zero velocity.

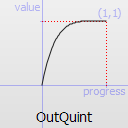
Easing curve for a quintic (t^5) function: decelerating to zero velocity.

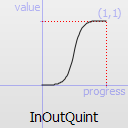
Easing curve for a quintic (t^5) function: acceleration until halfway, then deceleration.

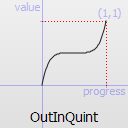
Easing curve for a quintic (t^5) function: deceleration until halfway, then acceleration.

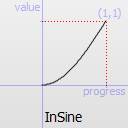
Easing curve for a sinusoidal (sin(t)) function: accelerating from zero velocity.

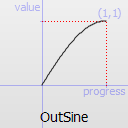
Easing curve for a sinusoidal (sin(t)) function: decelerating to zero velocity.

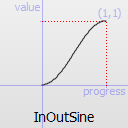
Easing curve for a sinusoidal (sin(t)) function: acceleration until halfway, then deceleration.

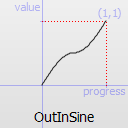
Easing curve for a sinusoidal (sin(t)) function: deceleration until halfway, then acceleration.

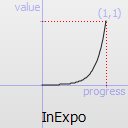
Easing curve for an exponential (2^t) function: accelerating from zero velocity.

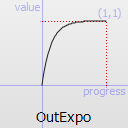
Easing curve for an exponential (2^t) function: decelerating to zero velocity.

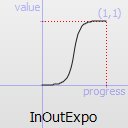
Easing curve for an exponential (2^t) function: acceleration until halfway, then deceleration.

Easing curve for an exponential (2^t) function: deceleration until halfway, then acceleration.

Easing curve for a circular (sqrt(1-t^2)) function: accelerating from zero velocity.

Easing curve for a circular (sqrt(1-t^2)) function: decelerating to zero velocity.

Easing curve for a circular (sqrt(1-t^2)) function: acceleration until halfway, then deceleration.

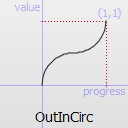
Easing curve for a circular (sqrt(1-t^2)) function: deceleration until halfway, then acceleration.

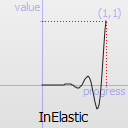
Easing curve for an elastic (exponentially decaying sine wave) function: accelerating from zero velocity. The peak amplitude can be set with the amplitude parameter, and the period of decay by the period parameter.

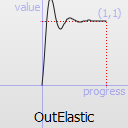
Easing curve for an elastic (exponentially decaying sine wave) function: decelerating to zero velocity. The peak amplitude can be set with the amplitude parameter, and the period of decay by the period parameter.

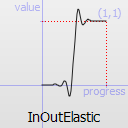
Easing curve for an elastic (exponentially decaying sine wave) function: acceleration until halfway, then deceleration.

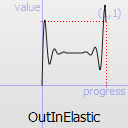
Easing curve for an elastic (exponentially decaying sine wave) function: deceleration until halfway, then acceleration.

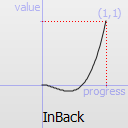
Easing curve for a back (overshooting cubic function: (s+1)*t^3 - s*t^2) easing in: accelerating from zero velocity.

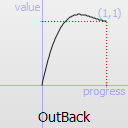
Easing curve for a back (overshooting cubic function: (s+1)*t^3 - s*t^2) easing out: decelerating to zero velocity.

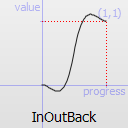
Easing curve for a back (overshooting cubic function: (s+1)*t^3 - s*t^2) easing in/out: acceleration until halfway, then deceleration.

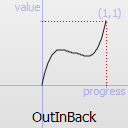
Easing curve for a back (overshooting cubic easing: (s+1)*t^3 - s*t^2) easing out/in: deceleration until halfway, then acceleration.

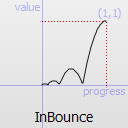
Easing curve for a bounce (exponentially decaying parabolic bounce) function: accelerating from zero velocity.

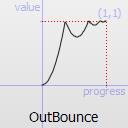
Easing curve for a bounce (exponentially decaying parabolic bounce) function: decelerating from zero velocity.

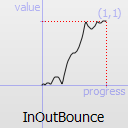
Easing curve for a bounce (exponentially decaying parabolic bounce) function easing in/out: acceleration until halfway, then deceleration.

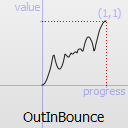
Easing curve for a bounce (exponentially decaying parabolic bounce) function easing out/in: deceleration until halfway, then acceleration.

See also

addCubicBezierSegment()addTCBSegment().

Member	Value	Description
BezierSpline	TODO	Allows defining a custom easing curve using a cubic bezier spline
CosineCurve	TODO	TODO
Custom	45	This is returned if the user specified a custom curve type with setCustomType(). Note that you cannot call setType() with this value, but type() can return it.
InBack	TODO	TODO
InBounce	TODO	TODO
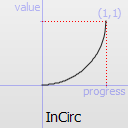
InCirc	TODO	TODO
InCubic	TODO	TODO
InCurve	TODO	TODO
InElastic	TODO	TODO
InExpo	TODO	TODO
InOutBack	TODO	TODO
InOutBounce	TODO	TODO
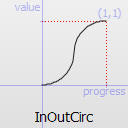
InOutCirc	TODO	TODO
InOutCubic	TODO	TODO
InOutElastic	TODO	TODO
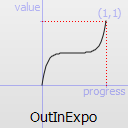
InOutExpo	TODO	TODO
InOutQuad	TODO	TODO
InOutQuart	TODO	TODO
InOutQuint	TODO	TODO
InOutSine	TODO	TODO
InQuad	TODO	TODO
InQuart	TODO	TODO
InQuint	TODO	TODO
InSine	TODO	TODO
Linear	TODO	TODO
OutBack	TODO	TODO
OutBounce	TODO	TODO
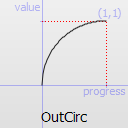
OutCirc	TODO	TODO
OutCubic	TODO	TODO
OutCurve	TODO	TODO
OutElastic	TODO	TODO
OutExpo	TODO	TODO
OutInBack	TODO	TODO
OutInBounce	TODO	TODO
OutInCirc	TODO	TODO
OutInCubic	TODO	TODO
OutInElastic	TODO	TODO
OutInExpo	TODO	TODO
OutInQuad	TODO	TODO
OutInQuart	TODO	TODO
OutInQuint	TODO	TODO
OutInSine	TODO	TODO
OutQuad	TODO	TODO
OutQuart	TODO	TODO
OutQuint	TODO	TODO
OutSine	TODO	TODO
SineCurve	TODO	TODO
TCBSpline	TODO	Allows defining a custom easing curve using a TCB spline

Methods

__init__(type: Type = Linear)

Constructs an easing curve of the given type.

---

__init__(Union[QEasingCurve, Type])

Construct a copy of other.

---

addCubicBezierSegment(Union[QPointF, QPoint], Union[QPointF, QPoint], Union[QPointF, QPoint])

TODO

---

addTCBSegment(Union[QPointF, QPoint], float, float, float)

TODO

---

amplitude() → float

Returns the amplitude. This is not applicable for all curve types. It is only applicable for bounce and elastic curves (curves of type() InBounce, OutBounce, InOutBounce, OutInBounce, InElastic, OutElastic, InOutElastic or OutInElastic).

See also

setAmplitude().

---

customType() → Callable[[float], float]

Returns the function pointer to the custom easing curve. If type() does not return Custom, this function will return 0.

See also

setCustomType().

---

__eq__(Union[QEasingCurve, Type]) → bool

TODO

---

__ne__(Union[QEasingCurve, Type]) → bool

TODO

---

overshoot() → float

Returns the overshoot. This is not applicable for all curve types. It is only applicable if type() is InBack, OutBack, InOutBack or OutInBack.

See also

setOvershoot().

---

period() → float

Returns the period. This is not applicable for all curve types. It is only applicable if type() is InElastic, OutElastic, InOutElastic or OutInElastic.

See also

setPeriod().

---

setAmplitude(float)

Sets the amplitude to amplitude.

This will set the amplitude of the bounce or the amplitude of the elastic “spring” effect. The higher the number, the higher the amplitude.

See also

amplitude().

---

setCustomType(Callable[[float], float])

TODO

---

setOvershoot(float)

Sets the overshoot to overshoot.

0 produces no overshoot, and the default value of 1.70158 produces an overshoot of 10 percent.

See also

overshoot().

---

setPeriod(float)

Sets the period to period. Setting a small period value will give a high frequency of the curve. A large period will give it a small frequency.

See also

period().

---

setType(Type)

Sets the type of the easing curve to type.

See also

type().

---

swap(QEasingCurve)

TODO

---

toCubicSpline() → List[QPointF]

TODO

---

type() → Type

Returns the type of the easing curve.

See also

setType().

---

valueForProgress(float) → float

Return the effective progress for the easing curve at progress. Whereas progress must be between 0 and 1, the returned effective progress can be outside those bounds. For example, InBack will return negative values in the beginning of the function.